
Details und Erläuterungen
Vermessung und Bau der ägyptischen Pyramiden - von Eckart Unterberger

Die Einmessung des rechten Winkels
Die Halbkreismethode
Man beginnt mit einer Grundlinie der Pyramide und bestimmt einen Eckpunkt. Von diesem Eckpunkt aus werden dann in gleichem Abstand zwei Hilfspunkte gemessen. Von diesen Punkten aus werden mit Hilfe eines Seiles zwei Kreisbögen geschlagen. Verbindet man den Schnittpunkt der beiden Kreisbögen mit dem Eckpunkt der Pyramide, so steht die Linie in rechtem Winkel auf die Kantenlinie.
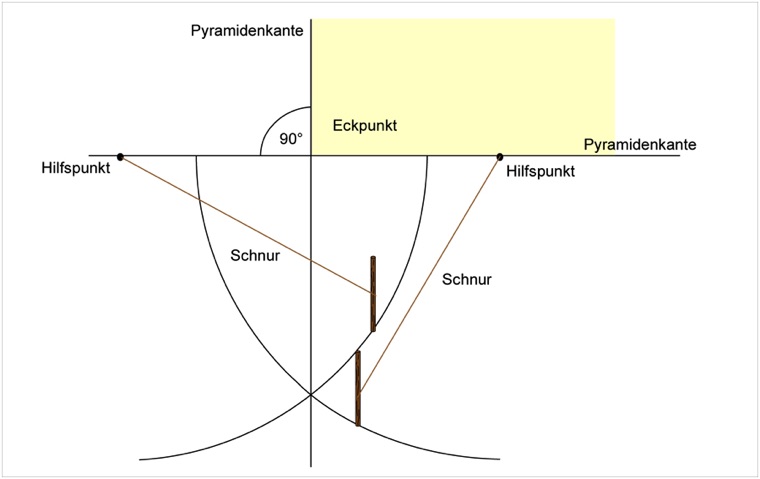
Die Methode entspricht jener, die jeder in der Schule lernt und auf einem A4 Blatt mittels Lineal und Zirkel mit hinreichender Genauigkeit auch ausführen kann. Ist die Genauigkeit aber auch für eine Kante von 230 m Länge entsprechend groß?
Um einen einigermaßen präzisen rechten Winkel zu erhalten, muss sich der Schnittpunkt in größerer Entfernung vom Eckpunkt befinden, da diese Linie verlängert werden soll. Nehmen wir an, er befindet sich in 50 m Entfernung.
Man benötigt rund um die Ecke der Pyramide ein 50 m x 50 m großes, ebenes Gelände. Die Schnur, die man als Zirkel zum Abschlagen der beiden Halbkreise verwendet, ist etwa 70 m lang.
Das Gelände lässt sich noch finden, bei der Schnur wird es schon schwieriger. Diese muss, um wie ein Zirkel zu funktionieren, konstant gespannt sein und in der Luft hängen. Dass dies nicht so einfach möglich ist, wurde bereits beschrieben. Zusätzlich muss der Stab, der als Stift funktioniert, während der Messung konstant senkrecht gehalten werden, was die Sache nicht gerade erleichtert und die Methode zu unpräzise werden lässt.





